Recently I came across this video from Kaggle Days Paris 2019 conference and found it very insightful. In this article, I will share all the unusual ML techniques mentioned in the video. These techniques can be immensely helpful in improving your ML model's performance for Kaggle competitions or real-world challenges such as credit scoring or high-frequency trading (HFT) 😮.

About the Speaker

TL;DR (public info from his Linkedin):

1. Stanislav Semenov is a former top-1 on Kaggle (which basically means he is one of the top data scientists in the world).
2. After success on Kaggle, he joined HFT fund for 2 years.
3. This video was released 2 years after his career in HFT fund and 1 year before founding his own trading firm Eqvilent.

I personally believe that the hacks he shared stem not only from his Kaggle experience but also from his work in the HFT fund. In the video he said:

All these tips & tricks are useful for real business problems (0:29)

Couple words about myself

I don't have any HFT-related experience but I have couple Kaggle medals and tried to build my own trading bots (but failed to generate any income). In this article I'll tell about the techniques he mentioned in the video but also my thoughts on how they can be used in Algorithmic Trading strategies. These are just my wild guesses and I'd be happy if you can share more practical approaches in comments anywhere.

ML tricks for Kaggle & HFT

Winsorization (0:54)

Limiting extreme values to reduce the effect of possible outliers.

All values below 1st percentile set to 1st percentile, and above 99th percentile -- to 99th percentile. You can find this function in scipy.stats module.

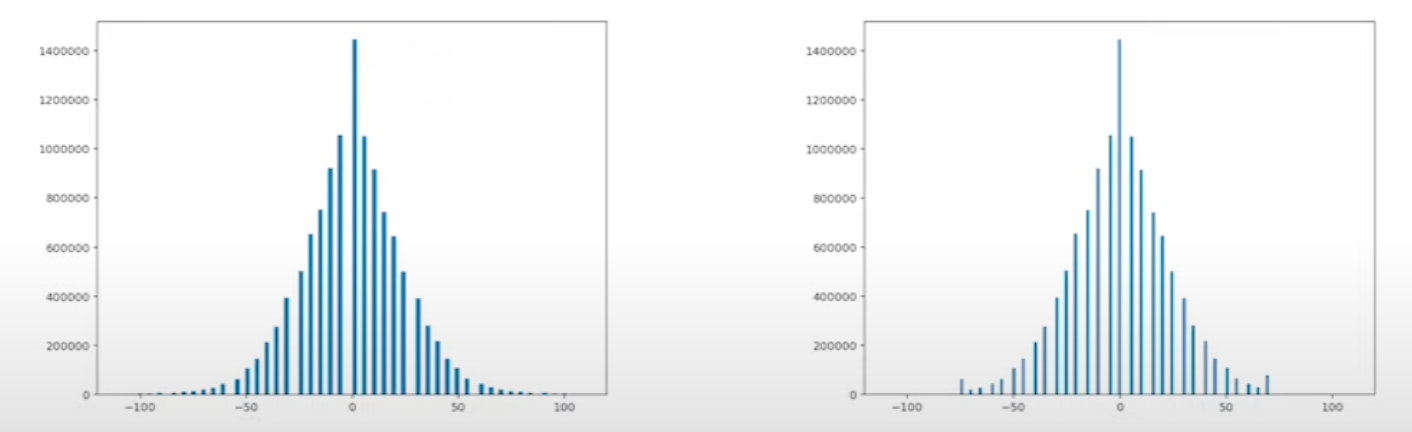
Even if there are only 7k results on Google with search query "Winsorization HFT", the technique looks like it is commonly used since helps ML/stats models converge faster.

Target Transformation (2:14)

This sounds more like a Kaggle-only hack but still...

Instead of attempting to predict your raw target, consider predicting different transformations of the target variable, such as y, log(y), log(y+1), y ** 2, y ** 0.5, or any other non-linear function of y. Depending on the loss function used, this approach may enhance your ML model's predictive performance.

Also, instead of predicting just y, you add multiple outputs for your NN model to predict y, sqrt(y), y ** 2 at the same time. This technique not only simplifies the task for the ML model but also serves as a form of regularization, enhancing its overall performance.

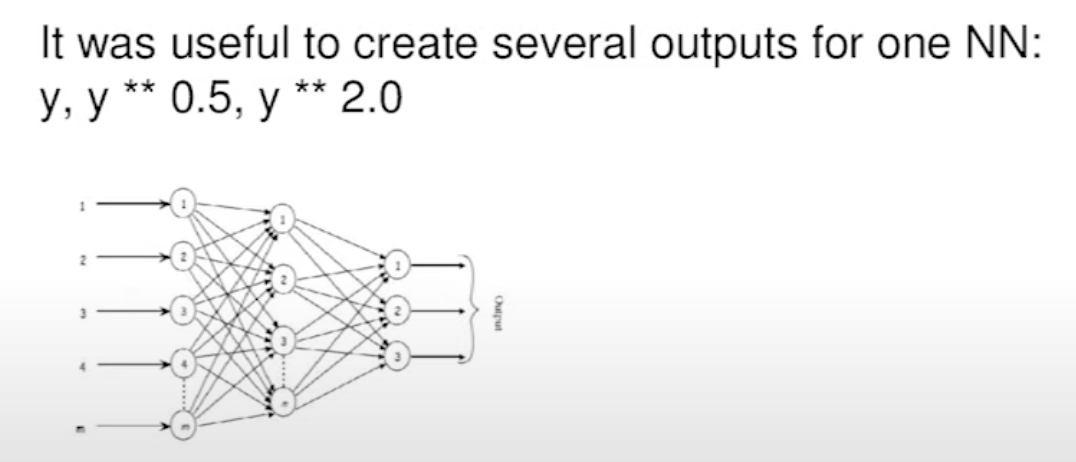
Prediction Transformation (3:21)

When dealing with a target variable within the range [0, 1], it's common for ML models to predict values clustering around 0.5. To encourage your ML model to make predictions closer to 0 or 1, you can apply this transformation that shifts values around 0.5 towards the respective edges:

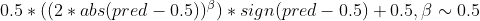
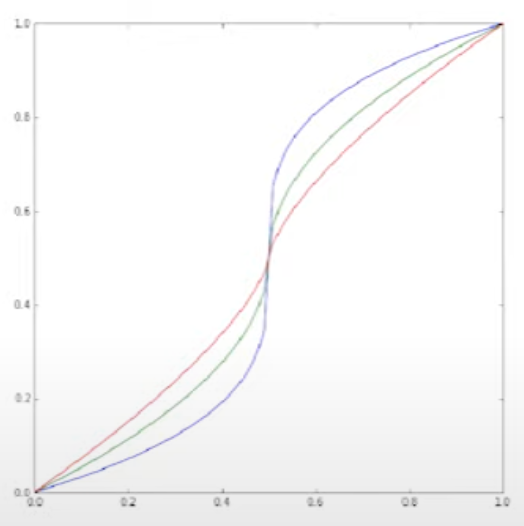
Linear Regression as a feature selection (4:03)

Imagine that you have a very big sparse matrix: ~10M features and ~1M objects (a common scenario in NLP tasks involving n-grams). Your goal is to identify the most impactful features efficiently. While the popular approach of using Tree-based algorithms and their feature importance metrics can be slow and suboptimal in this context, you can adopt an alternative strategy.

The solution is to fit simple Linear regression with L1 regularisation (should be pretty fast), select the most important features (in our example ~1k) and then train a tree-based algorithm (like xgboost) on the best features.

Train Data sampling: External Bagging (5:00)

I hope I understood that technique correctly...

Classic Bagging technique: fit a model on a random subset of a training data, repeat several times and average the predictions.

External Bagging:

1. Take a subset of all training data (size L)
2. Add Alpha * L more samples, e.g. Alpha = 2
3. Train, predict
4. Repeat k times, average predictions
5. Find proper Alpha with proper validation

Since Bagging is quite popular part of Random Forrest ML model, people usually think Bagging is suitable for Tree-based models only. But in practice, it is suitable for all machine learning models. And External Bagging too.

Train Data sampling: Time series (6:01)

Finally time series! Sounds like a real world example from Hedge fund practice.

Usually, in large time series (like prices in orderbook streams from an exchange) near objects are pretty similar. So the models tend to find more local dependencies rather than global.

To avoid this, we can select every k-th element as a training data. Do this k times, average the results and you may have a much better predictions.

Feature generation for Linear models (7:03)

Wait, hold on! Listen. Stanislav just said:

Imagine that we can use only Linear models and have only one feature.

Ha-ha. I know. This sounds like a mean price prediction for HFT. X is time and Y is price.

So our goal is to build the best Linear model possible even if the target is not linear at all (see screenshot below). The solution is to add more non-linear features to help our Linear model to approximate the price curve.

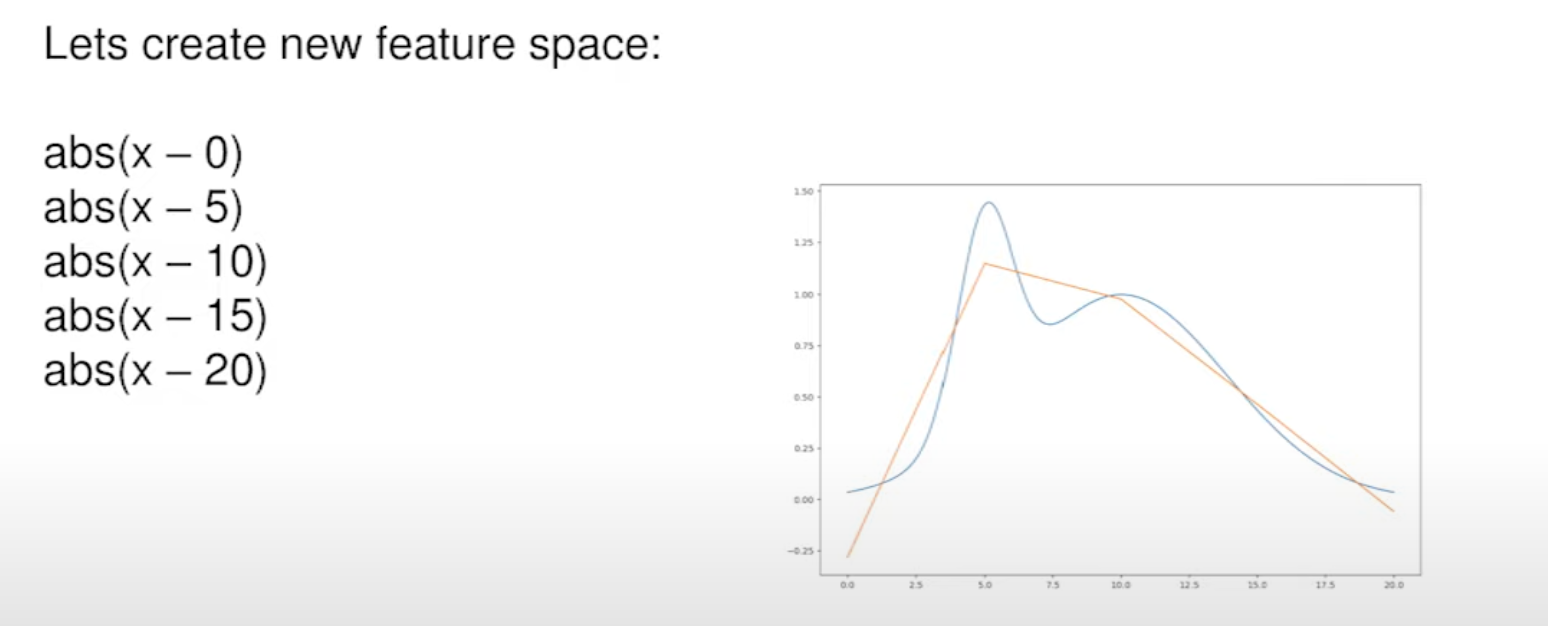
We can use these functions to create a new feature space for linear model:

1. abs(x - a)
2. sign(x - a)
3. (x - a) ** alpha

And if you have more that 1 feature:

1. (x1 - a) ** 2 + (x2 - b) ** 2
2. (x1 - a) >= 0 & (x2 - b) < 0

Note that the last feature looks like leaves from a tree-based model. To find the best constants for the formula, you can train a Tree-based model and extract weights from it.

How this can be used in HFT? My guess

On his screenshot above, x is definitely a time dimension and y is the price (or other financial metric). x = 0 is a current time. We want to predict (approximate linearly) the future price movement (for x > 0) based on the data from the past (x < 0). We use linear models to make our predictions in realtime and can use Train Data Sampling technique (mentioned above) to generate a train dataset (take price every 5 seconds or orderbooks).

Simple similarity feature (10:13)

Sometimes you just need to have more features in your dataset. In any scenario with any type of data you can add a Normalized Compressed Distance which basically compares the sizes of gzipped objects.

Isotonic Regression (12:06)

If you're sure your time series data doesn't decrease over time, you can use Isotonic Regression to make sure your predictions also follow this pattern. This model can be used in post-processing: you can quickly fix the predictions from other model (blue line on screen below) which may be not monotonic.

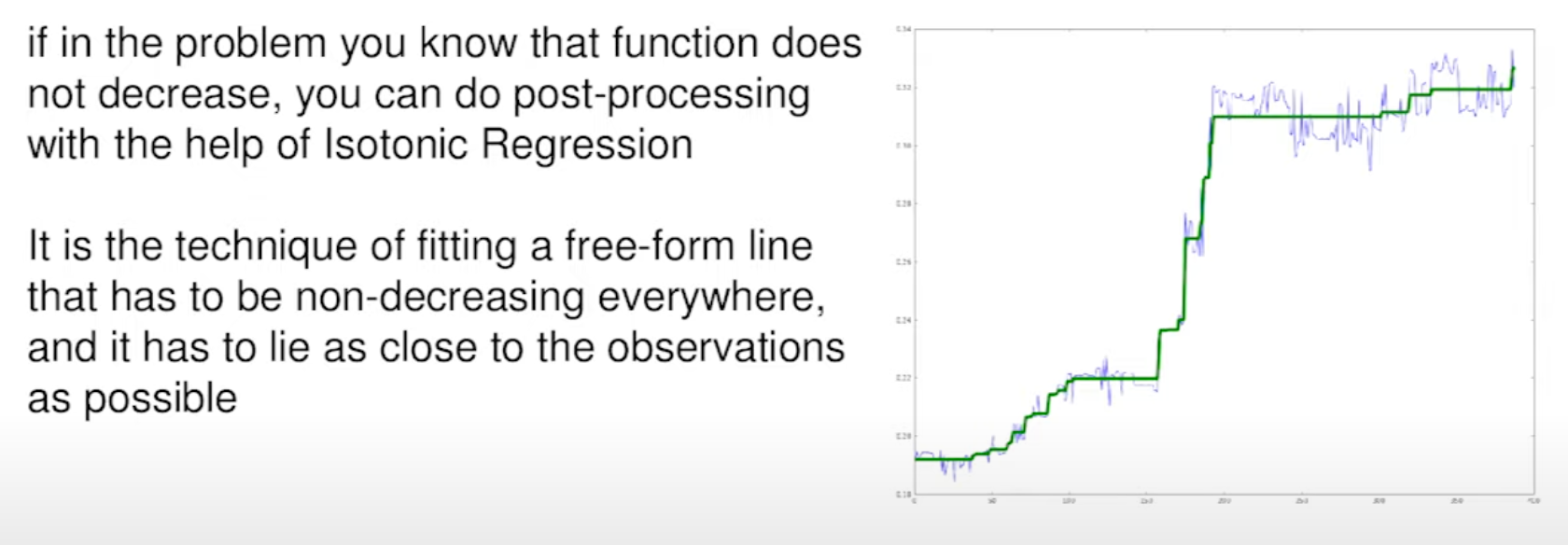
In HFT world, you probably can predict the price trend with Linear models (see above) and if some part of a time series probably be monotonic, you can improve the predictions with Isotonic Regression. Please share more insights on the trading applications of Isotonic Regression (if you are allowed to).

Thanks for reading! Please share this and leave a comment on Twitter, Telegram or Linkedin.